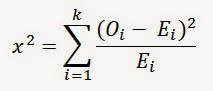UJI
NORMALITAS MENGGUNAKAN
UJI CHI
KUADRAT, UJI KOLMOGOROF SMIRNOV (KS) DAN UJI LILIEFORS]
A. Uji
Normalitas – Chi Kuadrat ( X2)
Uji normalitas dengan menggunakan
uji Chi Kuadrat disebut juga Uji Goodness of Fit. Menggunakan pendekatan
penjumlahan penyimpangan data observasi tiap kelas dengan nilai yang diharapkan.
Uji normalitas datanya disajikan secara berkelompok. Data berbentuk nominal
atau ordinal.
Ciri-Ciri
Distribusi Chi Kuadrat
·
Selalu positif
·
df = k – 1, dimana k adalah jumlah kategori (variabel). Jadi
bentuk distribusi chi-kuadrat tidak ditentukan banyaknya sampel, melainkan
banyaknya derajat bebas.
·
Bentuk distribusi
chi-kuadrat menjulur positif. Semakin besar derajat bebas, semakin mendekati
distribusi normal. Rumus
umum :
Keterangan :
Oi = frekuensi hasil pengamatan pada klasifikasi ke-i
Ei = frekuensi yang diharapkan pada klasifikasi ke-i
Oi = frekuensi hasil pengamatan pada klasifikasi ke-i
Ei = frekuensi yang diharapkan pada klasifikasi ke-i
X2
= Nilai Chi-Kuadrat
Uji
normalitas dengan menggunakan Chi-Kuadrat dapat dilakukan dengan langkah-langkah
sebagai berikut :
1.
Mencari
nilai terbesar dan terkecil
- Mencari nilai rentang
- Mencari banyak kelas
- Mencari panjang kelas interval
(i)
- Membuat tabel distribusi
frekuensi
- Mencari rata-rata (mean)
- Mencari simpangan baku (standar
deviasi)
- Membuat daftar frekuensi yang
diharapkan dengan cara sebagai berikut :
Ø Menentukan batas kelas, yaitu ujung
bawah kelas interval dikurangi 0.5 dan kemudian ujung atas kelas interval
ditambah 0.5
Ø
Mencari nilai Z menggunakan batas
bawah dan batas atas kelas interval dengan rumus:
Ø Mencari luas 0-Z dari Tabel Kurva
Normal dari 0-Z dengan menggunakan Z hitung.
Ø Mencari selisih luas tiap kelas
interval dengan cara mengurangkan nilai-nilai 0-Z tepi bawah dengan tepi atas.
9.
Mencari
frekuensi yang diharapkan dengan cara mengalikan luas tiap interval
dengan jumlah responden.
10.
Mencari
Chi-Kuadrat hitung
1.
Membandingkan
nilai X2 hitung dengan X2
tabel
Kriteria:
Jika X2 hitung
< X2 tabel maka H0 diterima dan untuk hal
lainnya H0 ditolak.
Contoh :
Akan diuji normalitas untuk data
Kemampuan Pemecahan Masalah Matematika Siswa Kelas VIII G SMP Negeri 407 Jepara
pada Materi Bangun Ruang. Apakah data tersebut berdistribusi normal?
Datanya adalah sebagai berikut :
No.
|
X
|
No.
|
X.
|
No.
|
X
|
No.
|
X
|
No.
|
X
|
1.
|
58
|
16.
|
51
|
31.
|
57
|
46.
|
72
|
61.
|
78
|
2.
|
57
|
17.
|
65
|
32.
|
51
|
47.
|
78
|
62.
|
71
|
3.
|
57
|
18.
|
85
|
33.
|
52
|
48.
|
66
|
63.
|
45
|
4.
|
51
|
19.
|
72
|
34.
|
51
|
49.
|
48
|
64.
|
50
|
5.
|
51
|
20.
|
78
|
35.
|
65
|
50.
|
71
|
||
6.
|
52
|
21.
|
58
|
36.
|
78
|
51.
|
78
|
||
7.
|
71
|
22.
|
59
|
37.
|
71
|
52.
|
70
|
||
8.
|
79
|
23.
|
58
|
38.
|
71
|
53.
|
65
|
||
9.
|
72
|
24.
|
64
|
39.
|
64
|
54.
|
37
|
||
10.
|
75
|
25.
|
64
|
40.
|
58
|
55.
|
58
|
||
11.
|
58
|
26.
|
58
|
41.
|
50
|
56.
|
50
|
||
12.
|
62
|
27.
|
71
|
42.
|
44
|
57.
|
50
|
||
13.
|
57
|
28.
|
64
|
43.
|
58
|
58.
|
58
|
||
14.
|
57
|
29.
|
78
|
44.
|
48
|
59.
|
48
|
||
15.
|
57
|
30.
|
78
|
45.
|
65
|
60.
|
67
|
||
Jawab :
Hipotesis :
H0 : data pada sampel berasal dari populasi
yang berdistribusi normal
H1 : data pada sampel berasal dari populasi
yang tidak berdistribusi normal
Langkah pengujiannya sebagai berikut :
1. Mencari nilai terbesar terbesar dan
terkecil
Nilai terbesar = 85
Nilai terkecil = 37
2. Mencari nilai rentang (R)
R = skor terbesar – skor terkecil
R = 85 – 37
= 58
3. Mencari banyak kelas (BK)
BK = 1 + 3,3 log n
BK = 1 + 3,3 log 64
BK = 1 + 3,3 (1,81)
BK = 1 + 3,3 (1,81)
BK = 1 + 5,973
BK = 6,973 dibulatkan menjadi 7
4. Mencari nilai panjang kelas (i)
1. Membuat tabel distribusi frekuensi
No
|
Kelas Interval
|
f
|
Nilai Tengah
(xi)
|
1.
|
37 - 44
|
2
|
40,5
|
2.
|
45 - 52
|
15
|
48,5
|
3.
|
53 - 60
|
16
|
56,5
|
4.
|
61 - 68
|
11
|
64,5
|
5.
|
69 - 76
|
11
|
72,5
|
6.
|
77 - 84
|
8
|
80,5
|
7.
|
85 - 92
|
1
|
88,5
|
jumlah
|
64
|
2. Mencari rata-rata (mean)
3. Mencari simpangan baku (standar
deviasi)
No.
|
Kelas
Interval
|
|||||
1.
|
37-44
|
2
|
40,5
|
-21,25
|
451,5625
|
903,125
|
2.
|
45-52
|
15
|
48,5
|
-13,25
|
175,5625
|
2633,4375
|
3.
|
53-60
|
16
|
56,5
|
-5,25
|
27,5625
|
441
|
4.
|
61-68
|
11
|
64,5
|
2,75
|
7,5625
|
83,1875
|
5.
|
69-76
|
11
|
72,5
|
10,75
|
115,5625
|
1271,1875
|
6.
|
77-84
|
8
|
80,5
|
18,75
|
351,5625
|
2812,5
|
7.
|
85-92
|
1
|
88,5
|
26,75
|
715,5625
|
715,5625
|
64
|
8860
|
1. Membuat daftar frekuensi yang
diharapkan dengan cara sebagai berikut :
1)
Menentukan
Tepi Bawah dan Tepi Atas Kelas Intervalt :
No
|
Kelas Interval
|
Batas bawah kelas
|
Batas atas kelas
|
1.
|
37 - 44
|
36,5
|
44,5
|
2.
|
45 - 52
|
44,5
|
52,5
|
3.
|
53 - 60
|
52,5
|
60,5
|
4.
|
61 - 68
|
60,5
|
68,5
|
5.
|
69 - 76
|
68,5
|
76,5
|
6.
|
77 - 84
|
76,5
|
84,5
|
7.
|
85 - 92
|
84,5
|
92,5
|
2)
Mencari
nilai Z menggunakan Tepi Bawah dan Tepi Atas Kelas Interval
3). Mencari
selisih luas tiap kelas interval dengan cara mengurangkan nilai-nilai 0-Z tepi
bawah dengan tepi atas
1. Mencari frekuensi yang diharapkan
dengan cara mengalikan selisih luas tiap interval dengan jumlah responden
(n = 64)
Selisih Luas 0-Z
|
Ei
|
0,0569
|
3,64
|
0,1442
|
9,23
|
0,2385
|
15,26
|
0,2595
|
16,61
|
0,1768
|
11,32
|
0,0801
|
5,13
|
0,0226
|
1,45
|
Frekuensi yang Diharapkan
(Ei) dari Hasil Pengamatan (Oi) untuk Variabel Kemampuan Pemecahan
Masalah Matematika Siswa Kelas VIII G SMP Negeri 407 Jepara pada Materi Bangun
Ruang
1. Mencari Chi-Kuadrat hitung
1. Membandingkan X2
hitung dengan X2 tabel
Dengan
membandingkan X2 hitung dengan nilai X2 tabel untuk
alpha =0,05 dan derajad kebebasan (dk) = k – 1 = 7 – 1 = 6, maka dicari
pada tabel Chi-Kuadrat didapat X2tabel = 12,6 dengan kriteria
pengujian sebagai berikut :
Jika X2 hitung
X2 tabel, artinya distribusi data
tidak normal
Jika X2
hitung < X2 , artinya data berdistribusi normal.
Ternyata X2
hitung < X2,atau 8,077 < 12,6 , maka H0 diterima.
Jadi, data Kemampuan Pemecahan Masalah Matematika Siswa Kelas VIII G SMP Negeri
407 Jepara pada Materi Bangun Ruang adalah berdistribusi normal. Sehingga,
analisis uji selanjutnya dapat dilanjutkan.
Kurva daerah penerimaan H0
A. UJI KOLMOGOROV SMIRNOV
Metode
Kolmogorov-Smirnov tidak jauh beda dengan metode Lilliefors.
Uji Kolmogorov Smirnov digunakan untuk menguji apakah data itu berdistribusi
normal atau tidak.Langkah-langkah penyelesaian dan penggunaan rumus sama, namun
pada signifikansi yang berbeda. Signifikansi metode Kolmogorov-Smirnov
menggunakan tabel pembanding Kolmogorov-Smirnov, sedangkan metode Lilliefors
menggunakan tabel pembanding metode Lilliefors.
PERSYARATAN
a. Data berskala
interval atau ratio (kuantitatif)
b. Data tunggal / belum
dikelompokkan pada tabel distribusi frekuensi
c. Dapat untuk n besar
maupun n kecil.
HIPOTESIS UJI :
H0 : Data populasi berdistribusi normal
H1 : Data populasi berdstribusi tidak
normal.
SIGNIFIKANSI UJI :
nilai terbesar | ft -
Fs | dibandingkan dengan nilai tabel Lilliefors.
·
Jika Lhitung <
Ltabel, maka :
§ Ho diterima
§ H1 ditolak.
·
Jika Lhitung >
Ltabel , maka :
§ Ho ditolak
§ H1 diterima
|
FT = Probabilitas komulatif normal
FS = Probabilitas komulatif empiris
Dhitung = | ft - Fs |
Dtabel = D(α,n) dilihat pada tabel kolmogorof smirnov
|
TABEL NILAI KRITIS L
UNTUK UJI KOLMOGOROV SMIRNOV :
LANGKAH-LANGKAH
PENGUJIAN :
Suatu penelitian tentang jumlah hasil panen kedelai di 15
kecamatan di Kabupaten Gresik tercatat dalam kwintal 10, 13, 15, 11, 8, 16, 10,
11, 12, 9 ,11, 14, 9, 18 dan 12 kwintal. Selidikilah dengan α =5% , apakah data
tersebut diambil dari populasi yang berdistribusi normal ? Gunakan Uji
Kormogorov Smirnov.
Hipotesis Uji :
H0 = Sampel berasal dari populasi
yang berdistribusi normal.
H1 = Sampel berasal dari populasi
yang berdistribusi tidak normal.
1.
Urutkan data
dari yang terkecil ke yang terbesar lalu cari
rata-rata, simpangan baku (standar deviasi) dari sampel data.
Keterangan
:
Xi = Data ke-i
fi = Frekuensi ke-i
fi = Frekuensi ke-i
1. Mencari (Ztabel ) pada tabel distribusi
normal

1. Menentukan
Dhitung
Keterangan :
Xi = Angka pada
data
Z = Transformasi
dari angka ke notasi pada distribusi normal
FT = Probabilitas
komulatif normal
FS = Probabilitas
komulatif empiris
v Mencari
nilai D(α,n) dan Dmax dengan
α = 0,05 dan n = 15 maka diperoleh :
-
D(0,05,15) / Dtabel=
0,338
-
Dhitung = 0,161
-
Daerah kritis : Dhitung<Dtabel
H0 diterima karena Dhitung
< Dtabel atau 0,161 < O,338
v Kesimpulan
: jumlah hasil panen kedelai di 15 kecamatan di Kabupatn Gresik memiliki data
yang normal
UJI LILIEFORS
Uji
liliefors digunakan untuk menguji apakah data itu berdistribusi normal atau
tidak.
Tedapat persyaratan untuk menggunakan
mettode liliefors ini, yaitu:
1. Data
berskala interval atau ratio (kuantitatif).
2. Data
tunggal atau belum dikelompokkan pada tabel distribusi frekuensi.
3. Dapat
untuk n besar maupun n kecil.
HIPOTESIS
UJI :
H0 : Data populasi berdistribusi normal
H1 :
Data populasi berdstribusi tidak normal
SIGNIFIKANSI
UJI :
nilai terbesar |
F(zi) - S(zi) | dibandingkan dengan nilai tabel Lilliefors.
·
Jika Lhitung < Ltabel liliefors , maka :
§ Ho
diterima
§ H1
ditolak.
·
Jika Lhitung > Ltabel liliefors , maka :
§ Ho
ditolak
§ H1
diterima
F(Zi) = P(Zi ≤ Ztabel (peluang)
S(Zi) = proporsi Z1 , Z2 , Z3 , Z4 , ... Zn yang ≤
Zi .
Lhitung =
| F(zi) - S(zi) |
Ltabel liliefors = dilihat pada tabel liliefors
TABEL NILAI KRITIS L UNTUK UJI
LILIEFORS :
LANGKAH-LANGKAH PENGUJIAN :
Contoh :
misalkan sampel dengan data : 23, 27, 33, 40, 48, 48, 57, 59, 62, 68, 69, 70
telah diambil dari sebuah opulasi.
Hipotesis Uji :
H0
= Sampel berasal dari populasi yang berdistribusi normal.
H1
= Sampel berasal dari populasi yang berdistribusi tidak normal.
5. Urutkan data dari yang terkecil ke
yang terbesar lalu cari rata-rata, simpangan baku (standar deviasi) dari sampel
data.
7. Mencari (Ztabel ) pada tabel distribusi
normal